7710. Change
of Scenery
Every day you drive to work using the same roads as it is the
shortest way. This is efficient, but over time you have grown increasingly
bored of seeing the same buildings and junctions every day. So you decide to
look for different routes. Of course you do not want to sacrifice time, so the
new way should be as short as the old one. Is there another way that differs
from the old one in at least one street?
Input. The first line starts with three integers n, m
and k (1 ≤ k ≤ n ≤ 104, 0 ≤ m
≤ 106), where n is the number of junctions, m is the number of streets in your city
and k is the number of junctions you
pass every day.
The next line contains k integers, the (1-based) indices of the
junctions you pass every day. The first integer in this line will always be 1,
the last integer will always be n.
There is a shortest path from 1 to n
along the k junctions given.
m lines follow. The i-th of those lines contains three
integers ai, bi, ci and describes a street from junction ai to junction bi of length ci (1 ≤ ai, bi ≤ n,
1 ≤ ci ≤ 104). Streets are always undirected.
Note that there may be multiple
streets connecting the same pair of junctions. The shortest path given uses for
every pair of successive junctions a
and b a street of minimal length
between a and b.
Output. Print one line
containing “yes” if there is another way you can take without losing time and
“no” otherwise.
|
Sample input 1 |
Sample output 1 |
|
3 3 3 1 2 3 1 2 1 2 3 2 1 3 3 |
yes |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
4 5 2 1 4 1 2 2 2 4 1 1 3 1 3 4 2 1 4 2 |
no |
SOLUTION
graphs - Dijkstra
Algorithm analysis
The line with k
crossroads that you pass every day does not carry any information.
Let d be the length of the shortest path between
vertices 1 and n. In this problem it is
required to establish whether there is more than one path of length d between
vertices 1 and n.
Start Dijkstra’s algorithm from
the vertex 1. Create an array mult, where mult[i] = 1 if there is more than one path from the source to the i-th vertex. Otherwise, set mult[i] = 0. Consider the relaxation of an edge from v to to
of length cost. If dist[to] = dist[v] + cost, then
there is at least a second path from the start vertex to to. Set mult[to] = 1. In the case of relaxation set mult[to] = mult[v].
There is more than one path between vertices 1 and n if mult[n] = 1.
Example
Graphs given in samples, have the next
form.
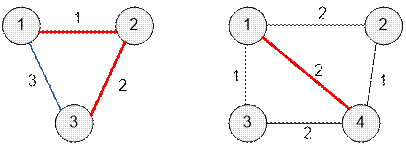
In the first
test there are two paths
of shortest length 3
between vertices 1 and 3. In the second test the length of the shortest path between 1 and 4 equals to 2. There is
no another path of
length 2 between vertices 1 and 4.
Algorithm realization
Declare a
constant infinity oo and arrays.
#define oo 0x3F3F3F3F
vector<int> used, dist, mult;
The edge structure
contains the information about the edge: vertex node where the edge runs and its length dist. The edge structure will
also be used in priority queue. The queue stores the vertices of the graph,
where
· node is the vertex number;
· dist is the current distnce from the source to the
vertex node.
The top of the queue will contain the vertex of the graph with the smallest dist value.
struct edge
{
int node,
dist;
edge(int
node, int dist) : node(node), dist(dist) {}
bool operator< (const
edge a) const
{
return dist
> a.dist;
}
};
Declare an adjacency
list of a graph g and a priority
queue pq for Dijkstra’s algorithm.
vector<vector<edge>
> g;
priority_queue<edge>
pq;
Relaxation of an edge running from v to to of length cost. If dist[to] = dist[v] + cost, then
there is at least a second path from the initial vertex to to. Set mult[to] = 1. In the case of relaxation, the
existence of more than one path to v
must lead to the existence of more than one path to to, set mult[to] = mult[v].
void
Relax(int v, int
to, int cost)
{
if (dist[to]
== dist[v] + cost)
mult[to] = 1;
if (dist[to]
> dist[v] + cost)
{
dist[to] = dist[v] + cost;
pq.push(edge(to,dist[to]));
mult[to] = mult[v];
}
}
The main part of the program. Read the input
data. Store the
weighted graph in the adjacency list g.
scanf("%d %d %d",&n,&m,&k);
for(i
= 0; i < k; i++) scanf("%d",&temp);
g.resize(n+1);
for(i
= 0; i < m; i++)
{
scanf("%d %d
%d",&a,&b,&w);
g[a].push_back(edge(b,w));
g[b].push_back(edge(a,w));
}
Initialize
the arrays.
dist.assign(n+1,oo);
dist[1]
= 0;
used.assign(n+1,0);
mult.assign(n+1,0);
Push the first
vertex into the
priority queue. Start
Dijkstra’s algorithm.
pq.push(edge(1,0));
while(!pq.empty())
{
edge e = pq.top(); pq.pop();
v = e.node;
If the vertex extracted from the queue is fictitious, then
do not process it.
if (e.dist
> dist[v]) continue;
Iterate and
relax the edges adjacent to the vertex v.
for(j = 0; j
< g[v].size(); j++)
{
to = g[v][j].node;
cost = g[v][j].dist;
if
(!used[to]) Relax(v,to,cost);
}
}
Print
the answer depending on the value of mult[n].
if
(mult[n] == 1)
puts("yes");
else
puts("no");
Java realization
import java.util.*;
class Node implements Comparator<Node>
{
public int node, dist;
Node() {}
Node(int node, int dist)
{
this.node = node;
this.dist = dist;
}
@Override
public int compare(Node a, Node b)
{
return a.dist - b.dist;
}
};
public class Main
{
// Adjacency
list representation of the edges
static
ArrayList<ArrayList<Node> > g;
static int dist[], mult[];
static int INF = Integer.MAX_VALUE;
static int n, m, k;
static void dijkstra(int start)
{
PriorityQueue<Node> pq = new
PriorityQueue<Node>(n+1, new Node());
for (int i = 0; i <= n; i++)
dist[i] = Integer.MAX_VALUE;
// Add source
node to the priority queue
pq.add(new Node(start, 0));
// Distance to
the source is 0
dist[start] = 0;
while(!pq.isEmpty())
{
Node e = pq.poll();
int v = e.node;
if (e.dist > dist[v]) continue;
for(int j = 0; j < g.get(v).size(); j++)
{
int to = g.get(v).get(j).node;
int cost = g.get(v).get(j).dist;
if (dist[v] + cost == dist[to]) mult[to] = 1;
if (dist[v] + cost < dist[to])
{
dist[to] = dist[v] + cost;
pq.add(new Node(to,dist[to]));
mult[to] = mult[v];
}
}
}
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
k = con.nextInt();
for(int i = 0; i < k; i++)
con.nextInt();
g = new
ArrayList<ArrayList<Node> >();
// Initialize
list for every node
for (int i = 0; i <= n; i++)
{
ArrayList<Node> item = new
ArrayList<Node>();
g.add(item);
}
for(int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
int w = con.nextInt();
g.get(a).add(new Node(b,w));
g.get(b).add(new Node(a,w));
}
dist = new int[n+1];
mult = new int[n+1];
dijkstra(1);
if (mult[n] == 1)
System.out.println("yes");
else
System.out.println("no");
con.close();
}
}